blogs

Weight-Decomposed Low-Rank Adaptation (DoRA): A Smarter Way to Fine-Tune LLMs

Haziqa Sajid

Haziqa Sajid

— 8 min read
Weight-Decomposed Low-Rank Adaptation (DoRA): A Smarter Way to Fine-Tune LLMs
Photo by Rick Rothenberg / Unsplash

Parameter-efficient fine-tuning (PEFT) methods address the challenge of fine-tuning large language models (LLMs) for specific downstream tasks when the cost of training all model parameters becomes prohibitive. 

Fine-tuning large language models with billions of parameters can be computationally expensive, require significant storage, and lead to overfitting, especially when adapting to tasks with limited data.

PEFT methods achieve efficiency by training a smaller subset of the total model parameters. This helps reduce the computational and memory requirements of fine-tuning.

Existing PEFT methods can be categorized into adapter-based methods, prompt-based methods, and LoRA variants.

Adapter-based methods add trainable modules to the model but increase inference latency. Prompt-based methods fine-tune input prompts, though they are sensitive to initialization.

LoRA uses low-rank matrices to approximate weight changes, avoiding architectural changes and extra latency.

Weight-Decomposed Low-Rank Adaptation (DoRA) is a novel PEFT method that builds upon LoRA by focusing on the directional component of weight updates.

This approach improves performance and closes the accuracy gap between LoRA and full fine-tuning (FT).

An Overview of DoRA | Source

In this article, we will explore DoRA in detail, including its decomposition method, implementation, and advantages.

LORA and its Limitations

Low-rank adaptation (LORA) is a parameter-efficient fine-tuning (PEFT) method used to adapt large language models (LLMs) for specific tasks without updating all the model parameters.

The weight updates made by LoRA during fine-tuning have a low intrinsic rank. It represents these changes using the product of two smaller matrices, denoted as B and A.

Given a pre-trained weight matrix, Wₒ LORA calculates the fine-tuned weight W' as:

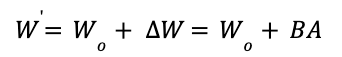
During training, only matrices B and A are trained, while Wₒ stays unchanged. This approach significantly reduces the number of trainable parameters compared to fine-tuning. 

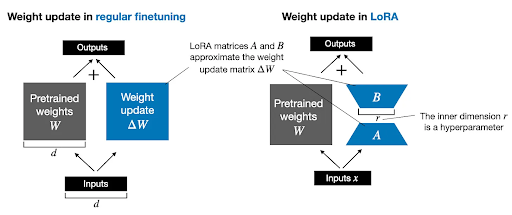
Illustration of Regular Finetuning (Left) and LoRA Finetuning (Right) | Source

Despite its advantages, LORA has limitations:

  • Performance Gap: LORA often exhibits lower accuracy than FT, which is typically attributed to its limited number of trainable parameters. 
  • Rank Selection: While increasing LORA's rank (size of matrices B and A) can improve its expressiveness, it may require extensive hyperparameter tuning.
  • Suboptimal Updates: The low-rank approximation might not always capture the optimal weight updates, potentially limiting the model's ability to adapt to the new task fully.

Understanding DoRA  

Before we get into DoRA (Weight-Decomposed Low-Rank Adaptation), it's important to understand the concept of decomposition.

Generally, it refers to breaking down a complex entity into simpler, more manageable components.

This approach in DoRA is inspired by Weight Normalization, a technique designed to improve the speed and stability of training deep neural networks. 

The Principle of Decomposition in DoRA

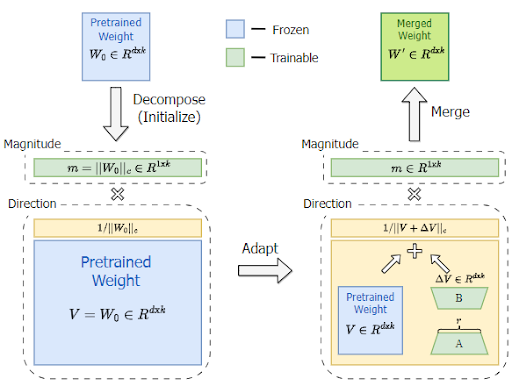
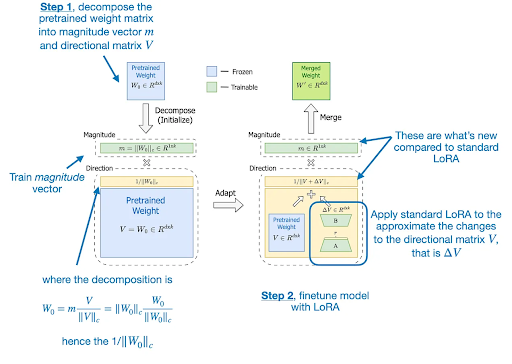
The central idea is to reparameterize the weight matrices into two separate components: magnitude and direction.

Instead of directly optimizing the weights, the algorithm updates these components separately.

Intuitively, the magnitude component controls the overall scale of the weights, while the direction component determines their orientation in the parameter space.

Weight Decomposition in DoRA

In DoRA, the weight decomposition is applied to the pre-trained weight matrix to optimize parameter fine-tuning.

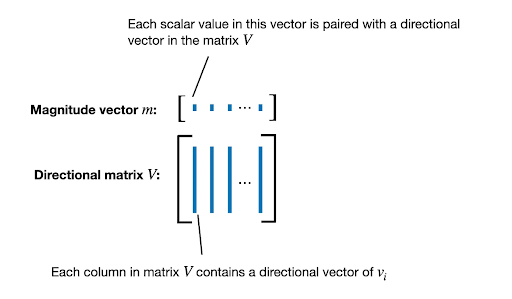
Each column of the weight matrix, which represents the weights associated with a specific neuron or feature, is decomposed into two components:

  • Magnitude: A scalar value that represents the length or norm of the weight vector.
  • Direction: A unit vector representing the weight vector's orientation in a high-dimensional space.

The weight decomposition of W can be formulated as:

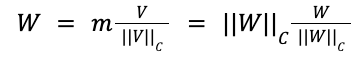
Here,

  • m is a row vector containing the magnitude scalars for each column of W.
  • V is the directional matrix, where each column is a unit vector.
  • ⎮⎮․⎮⎮𝑐 is the vector-wise norm of a matrix across each column.
Illustration of the Weight Matrix Decomposition in DoRA | Source

How DoRA Works

Now, to understand how DoRA works, let's see its core equation.

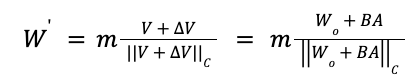
Where:

  • W': Final weight matrix after updates.
  • Wₒ: Original pre-trained weight matrix.
  • m: This is the magnitude component 
  • V: This is the directional component.
  • ∆V: This is the incremental update to the directional component introduced by LoRA.
  1. Initialization: The magnitude m and directional V components are initialized using the pre-trained weight matrix. LoRA's components (B and A) are initialized to make the initial change in direction ∆V zero.
  2. Magnitude Update: Only the magnitude component m is adjusted through gradient descent during training. This scalar scaling allows for flexible control over the overall strength of the weight vectors.
  3. Directional Adaptation with LoRA: The directional component is adapted through the low-rank update introduced by LoRA (BA). This modifies the orientation of the weight vectors without altering their magnitudes.
  4. Normalization: The updated directional component V + ∆V  is normalized to maintain unit length, ensuring that the magnitude component controls the weight vectors' scale.
  5. Merged Weight Matrix: The final updated weight matrix (W') is calculated by combining the adjusted magnitude m with the normalized, LoRA-adapted directional component.
How Weight-Decomposed Low-Rank Adaptation Works | Source

Gradient analysis is another important aspect of DoRA. By closely examining gradient patterns during training, DoRA identifies optimal directions for weight updates. This process improves the efficiency of fine-tuning and improves overall performance.

Let’s walk through the implementation of DoRA.

DoRA implementation with HuggingFace

We'll use the Hugging Face Transformers library and the PEFT library for our implementation, leveraging Hugging Face for LLMs. The PEFT library will facilitate efficient DoRA fine-tuning of pre-trained models with minimal computation.

Step 1: Install Necessary Libraries

Start by installing the required libraries transformers, PEFT (Parameter-Efficient Fine-Tuning), and datasets:


!pip install transformers
!pip install peft
!pip install datasets

Step 2: Import Libraries

Load the necessary packages and modules from Hugging Face’s transformers, datasets, and PEFT.


import torch
from transformers import AutoModelForCausalLM, AutoTokenizer, TrainingArguments, Trainer, AutoModelForCausalLM
from peft import LoraConfig, get_peft_model
from datasets import Dataset
import transformers

Step 3: Create Sample Question-Answer Dataset

For demonstration, we’ll create a small dataset of questions and answers along with relevant context.


# Sample QA Data
data = {
    'question': [
        "What is the capital of France?",
        "Who painted the Mona Lisa?",
        "What is the tallest mountain in the world?",
        "When did World War II end?",
        "Who wrote the play 'Romeo and Juliet'?",
        "What is the chemical symbol for gold?"
    ],
    'context': [
        "Paris is the capital and most populous city of France.",
        "The Mona Lisa is a half-length portrait painting by Italian Renaissance artist Leonardo da Vinci.",
        "Mount Everest is Earth's highest mountain above sea level, located in the Mahalangur Himal sub-range of the Himalayas.",
        "World War II (WWII or WW2), also known as the Second World War, was a global war that lasted from 1939 to 1945.",
        "Romeo and Juliet is a tragedy written by William Shakespeare early in his career about two young star-crossed lovers whose deaths ultimately reconcile their feuding families.",
        "Gold is a chemical element with the symbol Au and atomic number 79. In its purest form, it is a bright, slightly reddish yellow, dense, soft, malleable, and ductile metal."
    ],
    'answer': [
        "Paris",
        "Leonardo da Vinci",
        "Mount Everest",
        "1945",
        "William Shakespeare",
        "Au"
    ]
}
dataset = Dataset.from_dict(data)

Step 4: Load the Pre-trained Model and Tokenizer

Select a pre-trained model (e.g., GPT-2) for the question-answering task and load its tokenizer.


model_id = "gpt2"


# Load the tokenizer and model
tokenizer = AutoTokenizer.from_pretrained(model_id)
model = AutoModelForCausalLM.from_pretrained(model_id)


# Ensure padding token is set
if tokenizer.pad_token is None:
    tokenizer.add_special_tokens({'pad_token': '[PAD]'})

Step 5: Define LoRA Configuration with DoRA

Set up the configuration for LoRA and DoRA, enabling the weight decomposition used in DoRA.


peft_config = LoraConfig(
    r=8,
    lora_alpha=16,
    target_modules=["c_attn"],  
    lora_dropout=0.05,
    bias="none",
    task_type="CAUSAL_LM",
    use_dora =True # Enables DoRA
)


# Create PEFT Model
model = get_peft_model(model, peft_config)

Step 6: Preprocess the Data

Define a prompt generation function and apply it to the dataset to format each question, context, and answer.


# Preprocess Data
def generate_prompt(data_point):
    return f"""[INST] {data_point["question"]} [/INST] {data_point["context"]} {data_point["answer"]} [/INST]"""


dataset = dataset.map(lambda data_point: {"text": generate_prompt(data_point)})

Step 7: Tokenize the Data

Tokenize each prompt for input to the model.


# Tokenize Data
def tokenize(prompt):
    result = tokenizer(prompt["text"])
    return {
        "input_ids": result["input_ids"],
        "attention_mask": result["attention_mask"],
    }
tokenized_dataset = dataset.map(tokenize, batched=True, remove_columns=dataset.column_names)

Step 8: Set Training Arguments and Initialize the Trainer

Define training parameters suited for smaller hardware setups.


# Training Arguments (Optimized for CPU)
training_args = TrainingArguments(
    per_device_train_batch_size=1,  # Very small batch size for CPU
    gradient_accumulation_steps=8,  # Accumulate gradients over multiple steps
    num_train_epochs=3,
    learning_rate=1e-4,  # Smaller learning rate for CPU
    logging_steps=10,
    output_dir="./trained-dora",
    report_to="none"
)

Create a Trainer object to manage the fine-tuning process.


# Create Trainer
trainer = Trainer(
    model=model,
    train_dataset=tokenized_dataset,
    args=training_args,
    data_collator=transformers.DataCollatorForLanguageModeling(tokenizer, mlm=False),
)

Step 9: Fine-tune and Save the Model

Disable caching to save memory and start training.


# Fine-tune!
model.config.use_cache = False
trainer.train()

Save the trained model and tokenizer for future use.


# Save the Fine-tuned Model
model.save_pretrained("./trained-dora")
# Save the tokenizer as well to load it during inference.
tokenizer.save_pretrained("./trained-dora")

Step 10: Evaluate the Fine-Tuned Mode

Load the model and tokenizer to test the model and generate answers to questions.


# Code: Finetune Large Language Models with DoRA (Test).
import torch
from transformers import AutoModelForCausalLM, AutoTokenizer, GenerationConfig, TrainingArguments, Trainer
import transformers


# Load Fine-Tuned Model and Tokenizer
model_path = "./trained-dora"


# Now the tokenizer can be loaded using:
tokenizer = AutoTokenizer.from_pretrained(model_path)
model = AutoModelForCausalLM.from_pretrained(model_path)


# Ensure Model is on CPU
device = torch.device("cpu")
model.to(device)
if tokenizer.pad_token is None:
    # tokenizer.add_special_tokens({'pad_token': '[PAD]'})
    tokenizer.pad_token = tokenizer.eos_token


# Load Your Question-Answering Dataset (Replace with your dataset)
eval_data = [
    {"question": "What is the capital of France?", "context": "Paris is the capital and most populous city of France.", "answer": "Paris"},
    {"question": "Who painted the Mona Lisa?", "context": "The Mona Lisa is a half-length portrait painting by Italian Renaissance artist Leonardo da Vinci.", "answer": "Leonardo da Vinci"},
]


# Function to generate the prompt
def generate_prompt(data_point):
    return f"""[INST] {data_point["question"]} [/INST] {data_point["context"]} {data_point["answer"]} [/INST]"""


# Test the Model
for data_point in eval_data:
    input_text = generate_prompt(data_point)
    input_ids = tokenizer(input_text, return_tensors="pt").input_ids.to(device)  # Move input to CPU


    # Generate Answer
    generation_output = model.generate(
        input_ids=input_ids,
        max_new_tokens=50,  # Adjust as needed
        num_beams=1,  # You can try increasing num_beams if you have enough memory
        early_stopping=True,
    )


    # Extract and Print Answer
    generated_answer = tokenizer.decode(generation_output[0])
    print(f"Question: {data_point['question']}")
    print(f"Generated Answer: {generated_answer.split('[/INST]')[-2].strip()}")
    print(f"Actual Answer: {data_point['answer']}")

Output

Generated Output by DoRAs Fine-tuned Model

Benefits of DoRA Over Standard PEFT

DoRA has several benefits compared to other PEFT techniques, particularly LoRA. These advantages stem from DoRA's unique approach to decomposing the pre-trained weight matrices.

  • Improved Learning Capacity: DoRA exhibits a learning capacity closer to full fine-tuning (FT) than standard LoRA. When fine-tuning the LLaMA-7B model for commonsense reasoning, DoRA achieves a 3.7% accuracy improvement over LoRA.
  • Reduced Overfitting: DoRA generalizes better, particularly in low-data scenarios, by focusing on specific weight components.
  • Reduced Training Overhead: DoRA further reduces memory requirements beyond PEFT without sacrificing accuracy. The Gradient Detachment modification reduces training memory by about 24.4% for LLaMA and 12.4% for VL-BART, with minimal impact on accuracy.

Conclusion

DoRA improves PEFT by addressing LoRA's limitations and providing a more efficient way to fine-tune large language models. 

It achieves superior performance while maintaining PEFT's computational benefits by combining weight decomposition with advanced gradient analysis.

This guide demonstrated the implementation of DoRA with HuggingFace by fine-tuning a GPT-2 model to help you better understand its practical application. 

Read more